Tensorflow ロジスティック回帰による二項分類器（マイナビ本参考）

◆ 目的：
ウィルスの感染を分類する、したい。

◆ キーワード：
ロジスティック回帰、二項分類器、境界線、直線、確率0.5、シグモイド関数、データのランダム生成、確率の最大化、最尤推定法、統計学、誤差関数、log、pandas、DateFrame、行列T、ブロードキャスト、グラフの描画、濃淡、スパム、感染非感染、学習

・まずは、インポート・準備

# ロジスティック回帰の二項分類器、65頁参考

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt

# 乱数を使ってデータ生成、pandasのデータフレームとして格納

from numpy.random import multivariate_normal, permutation
import pandas as pd
from pandas import DataFrame, Series

・感染データ/非感染データを作る

# データを用意
# 感染していないデータ（t=0）の生成

np.random.seed(20170602)

n0, mu0, variance0 = 20, [10, 11], 20
data0 = multivariate_normal(mu0, np.eye(2)*variance0 ,n0)
df0 = DataFrame(data0, columns=['x1','x2'])
df0['t'] = 0

# 感染しているデータ（t=1）の生成
n1, mu1, variance1 = 15, [18, 20], 22
data1 = multivariate_normal(mu1, np.eye(2)*variance1 ,n1)
df1 = DataFrame(data1, columns=['x1','x2'])
df1['t'] = 1

df = pd.concat([df0, df1], ignore_index=True)

# データセット
# 上で生成したデータを表示して内容を確認、３５コのサンプルデータ

train_set = df.reindex(permutation(df.index)).reset_index(drop=True)
train_set

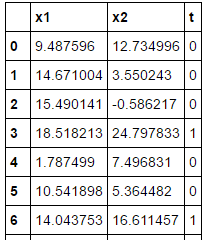
・変数を定義

# Tensorflowで計算できるようにデータを変形
# numpyのarrayオブジェクトとして変数に格納
# X・・・（ｘ１ｎ、ｘ２ｎ）の行列　、　ｔ・・・正解ラベル

train_x = train_set[['x1','x2']].as_matrix()
train_t = train_set['t'].as_matrix().reshape([len(train_set),1])

# Step１_予測のための数式定義
#　確率Pを行列形式で計算
# f = x*w + w0
# 入力データは３５行２列 but Noneでサイズ規定
# ｗは、ｗ　=　（ｗ１，ｗ２）T 転置 ・・・横のw１、ｗ２を縦に並べている　２行１列
# w０は、ブロードキャスト・・・１次元リストでも足せる
# ｔｆ．sigmoidはそれぞれの入力に対するシグモイド関数の一次元リスト

x = tf.placeholder(tf.float32, [None, 2])
w = tf.Variable(tf.zeros([2,1]))
w0 = tf.Variable(tf.zeros([1]))

f = tf.matmul(x,w) + w0

p = tf.sigmoid(f)

・誤差関数を定義

# Step2_誤差関数定義
# 数式自体は-logPを掛け合わていくような複雑なやつ,Σで表現＠p７０
# tf. reduce_sumは和集約

t= tf.placeholder(tf.float32, [None, 1])
loss = -tf.reduce_sum(t*tf.log(p) + (1-t)*tf.log(1-p))

# アダムオプティマイザーで上で定義したloss関数を最小化していく

train_step = tf.train.AdamOptimizer().minimize(loss)

・予測

#　正解ｏｒ不正解の分別 Pn＞＝0.5であればｔ＝１
#  tf.sign  符号を取り出す関数
# tf.equal  引数が等しいかを判定する関数 Bool値を返す
# ブロードキャストルールによって、Bool値の縦ベクトルが生成される

correct_prediction = tf.equal(tf.sign(p-0.5), tf.sign(t-0.5))

# tf．cast　　Bool値を１，０の値に変換
# tf.reduce_mean  ベクトルの各成分の平均値、正解なら１、不正解なら０

accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))

#　パラメータの最適化
sess = tf.Session()
sess.run(tf.global_variables_initializer())

・勾配降下法

# 勾配降下法 ２００００回繰り返し

i = 0
for _ in range(20000):
    i += 1
    sess.run(train_step, feed_dict={x:train_x, t:train_t})
    
    if i % 2000 == 0:
        loss_val, acc_val = sess.run([loss, accuracy], feed_dict={x:train_x, t:train_t})
        print('Step: %d, Loss %f, Accuracy: %f' % (i, loss_val, acc_val))

（out）
Step: 2000, Loss 16.098034, Accuracy: 0.857143
Step: 4000, Loss 12.176691, Accuracy: 0.885714
Step: 6000, Loss 9.802266, Accuracy: 0.914286
Step: 8000, Loss 8.280571, Accuracy: 0.914286
Step: 10000, Loss 7.283283, Accuracy: 0.914286
Step: 12000, Loss 6.632703, Accuracy: 0.914286
Step: 14000, Loss 6.220951, Accuracy: 0.914286
Step: 16000, Loss 5.976564, Accuracy: 0.914286
Step: 18000, Loss 5.848728, Accuracy: 0.914286
Step: 20000, Loss 5.797661, Accuracy: 0.942857

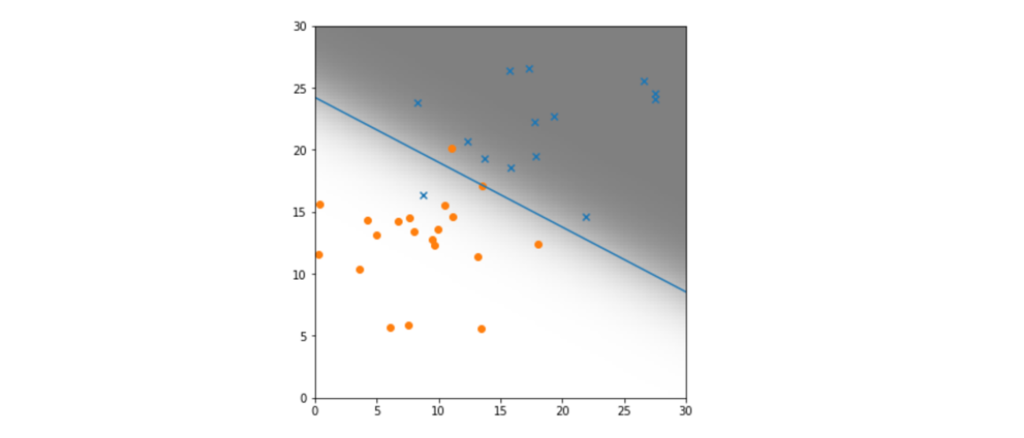
# Variableの値を取得
# w0・・・１要素のみのリスト
# ｗ　・・・２行１列の行列
# ［０］［０］は一行目を取り出し、［１］［０］は２行目を取り出し

w0_val, w_val = sess.run([w0, w])
w0_val, w1_val, w2_val = w0_val[0], w_val[0][0], w_val[1][0]

print (w0_val, w1_val, w2_val)
-14.9617 0.322867 0.617867

# 結果をグラフに表示
# 境界線は、P（ｘ１，ｘ２）=０．５ の確率
#　シグモイド関数はロジスティック関数とも。ロジスティック回帰。

#トレーニングセットのデータからt=０、１のデータを個別に取出し

train_set0 = train_set[train_set['t']==0]
train_set1 = train_set[train_set['t']==1]

#　散布図の記号etc

fig = plt.figure(figsize=(6,6))
subplot = fig.add_subplot(1,1,1)
subplot.set_ylim([0,30])
subplot.set_xlim([0,30])
subplot.scatter(train_set1.x1, train_set1.x2, marker='x')
subplot.scatter(train_set0.x1, train_set0.x2, marker='o')

・グラフの細かい描画設定

# 境界線の直線の描画

linex = np.linspace(0,30,10)
liney = - (w1_val*linex/w2_val + w0_val/w2_val)

subplot.plot(linex, liney)

# 確率の変化を濃淡で示す
# （ｘ１，ｘ２）平面を１００ｘ１００のセルに分割
# それぞれのセルの確率P(ｘ１、ｘ２)の値を２次元リスト filedに格納　濃淡表示

field = [[(1 / (1 + np.exp(-(w0_val + w1_val* x1 + w2_val*x2))))
         for x1 in np.linspace(0,30,100)]
        for x2 in np.linspace(0,30,100)]

subplot.imshow(field, origin= 'lower', extent = (0,30,0,30), cmap=plt.cm.gray_r, alpha=0.5)

plt.show()