Memo 用語&単語 etc

◆Python&機械学習関連の用語
・パーセプトロン…重み設定の作業が人手。活性化関数がステップ関数。@魚本
・ニューラルネットワーク…ニューロンのつながり方はパーセプトロンと何ら変わりなし。多層で、シグモイド関数などの滑らかな活性化関数を使用するネットワーク。@魚本
・活性化関数…入力信号の総和がどのように活性化(発火)するかを決める役割りを果すもの。@魚本
・正規化(normalization)…データをある決まった範囲に変換する処理@魚本
・損失関数(loss function)…「ニューラルネットワークの学習では、最適なパラメータ(重みとバイアス)を探索する際に、損失関数の値ができるだけ小さくなるようなパラメータを探します。」2乗和誤差、交差エントロピー誤差などを用いる。「できるだけ小さな損失関数の場所を探すために、パラメータの微分(正確には勾配)を計算し、その微分の値を手がかりにパラメータの値を徐々に更新していきます。」@魚本
・2乗和誤差…「ニューラルネットワークの出力と正解となる教師データの各要素の差の2乗を計算し、その総和を求めます。」@魚本
・偏微分…「…ある場所の傾きを求めます。ただし、…変数をひとつに絞り、他の変数はある値い固定します。」@魚本
・勾配…「すべての変数の偏微分をベクトルとしてまとめたもの」@魚本
・勾配法…「勾配をうまく利用して関数の最小値(または、できるだけ小さな値)を探そう、というのが勾配法です。」@魚本
・学習率(learning rate)…「1回の学習で、どれだけ学習すべきか、どれだけパラメータを更新するか、ということを決めるのが学習率です。」@魚本
・ハイパーパラメータ…人の手によって設定されるパラメータ
・誤差逆伝播法…「局所的な微分」の伝達@魚本
・畳込みフィルタ…「画像に描かれている物体の特徴をより的確に捉えることが可能になります」@中井マイナビ本、p27
・点でなく領域ベースで特徴抽出できるので移動変形に強くなる。また、エッヂ抽出など領域ベースでないと分からないような特徴も抽出可となる。@Qiita
・プーリング層…「画像の解像度を落とす処理を行います。…詳細をあえて消し去ることで、描かれている物体の本質的な特徴のみを抽出しようという発想に基づきます。」@中井マイナビ本、p27
・サイズを圧縮して後の層で扱いやすくできるメリット@Qiita
==未整理==
・broadcasting… 形状の違う配列どうしを計算。
・category表現…[0, 1, 2, 1, 0, 2]
・one-hot 表現…[ 1., 0., 0.] 要素1つが1で他が全て0
・リスト…要素のシーケンス、挿入&削除ができる、ミュータブル
a=[1,2,3]
print(a)
=>
[1, 2, 3]
・タプル…イミュータブル、変更不可
a=(1,2,3)
print(a)
=>
(1, 2, 3)
Python Numpyに慣れる100エクササイズ
◆ベクトルを作る・いじる

☞ ”array” ・・・要素指定で配列を生成する
print(np.array([[1, 2, 3], [4, 5, 6]]))
=>
[[1 2 3]
[4 5 6]]
☞ ”arange”・・・連番の配列を作る
print(np.arange(5)) # start = 0 (default), end = 5
print(np.arange(1,5)) # start = 1, end = 5
print(np.arange(1,5,0.5)) # start = 1, end = 5, slice = 0.5
=>
[0 1 2 3 4]
[1 2 3 4]
[ 1. 1.5 2. 2.5 3. 3.5 4. 4.5]
☞ ”flatten”・・・一次元化
W = np.array([[1, 2, 3], [4, 5, 6]])
print(W)
print(W.flatten())
=>
[[1 2 3]
[4 5 6]]
[1 2 3 4 5 6]
☞ ”reshape”・・・行列のかたちを変更
print(np.arange(48).reshape(8, 6))
=>

A = np.arange(24).reshape(2,3,4) #2つの行列に分ける
print(A)
=>
[[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
[[12 13 14 15]
[16 17 18 19]
[20 21 22 23]]]
☞ ”shape”・・・配列の値の数を得る
(1) 3x2行列.shape → (3,2)
(2)3x2行列.shape [0]→ 行の数 この例では3
ex:
X = np.arange(12).reshape(3,4)
print(X)
=>
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
ex:
print(X.shape)
print(X.shape[0])
=>
(3, 4) 3
ex:
b = np.array([2,4,6,8])
print(b.shape)
=>
(4,)
☞ ”zeros”・・・全部0の配列を作る (cf. 全部1なら”ones”)
Z1 = np.zeros(5) #一次元
Z2 = np.zeros*1 #2行3列のように形状指定もOK
print(Z1)
print(Z2)
=>
[ 0. 0. 0. 0. 0.]
[[ 0. 0. 0.]
[ 0. 0. 0.]]
・参考)4つ目が1
Z = np.zeros(10)
Z[4] = 1
print(Z)
=>
[ 0. 0. 0. 0. 1. 0. 0. 0. 0. 0.]
☞ ”np.random.choice()”・・・ランダム
・指定された数字の中からランダムに好きな数を取り出す
np.random.choice(100,3) #0〜99のうちランダムに3つ数字を抽出
=>
array([89, 41, 92])
◆ ”def”・・・関数を定義
def add(x, y):
print x + y
add(3, 5)
=> 8
◆ ”numpy.newaxis”・・・縦配置
(1)ヨコ→タテ
array = np.arange(5)
print (array[:, np.newaxis])
=>
[[0]
[1]
[2]
[3]
[4]]
(2)九九表を作る
m = np.array([1,2,3,4,5,6,7,8,9])
n = np.array([1,2,3,4,5,6,7,8,9])
print(m[:, np.newaxis]) # m配列を縦に
print(m[:, np.newaxis]*n) # それにn配列を掛け算していく

☞ その7・・・エレメントをリバースする
Z = np.arange(15)
Z = Z[::-1]
print(Z)
=>
[14 13 12 11 10 9 8 7 6 5 4 3 2 1 0]
☞ その8・・・3x3のマトリクス
Z = np.arange(9).reshape(3,3)
print(Z)
=>
[[0 1 2]
[3 4 5]
[6 7 8]]
☞ その9・・・ある行列からindexをさがす
nz = np.nonzero([1,2,0,0,4,0])
print(nz)
=>
(array([0, 1, 4], dtype=int64),)
☞ その10・・・identity matrix 単位行列
Z = np.eye(3)
print(Z)
=>
[[ 1. 0. 0.]
[ 0. 1. 0.]
[ 0. 0. 1.]]
☞ その11・・・3x3x3のランダム行列の作成
Z = np.random.random*2
print(Z)
=>
[[[ 0.86816012 0.54928482 0.10620469]
[ 0.56253858 0.42498644 0.38111299]
[ 0.46583937 0.06876381 0.47205835]]
[[ 0.48659812 0.53796306 0.83180752]
[ 0.54321802 0.2645361 0.6461197 ]
[ 0.69551154 0.60727098 0.36739499]]
[[ 0.31582316 0.86979075 0.77204474]
[ 0.93540842 0.18592936 0.17472491]
[ 0.87547108 0.59652846 0.87853689]]]
☞ その12・・・3x3のランダム行列を作り、その中の要素の最大値/最小値を抽出
Z = np.random.random*3
Zmin, Zmax = Z.min(), Z.max()
print(Z)
print(Zmin, Zmax)
=>
[[ 0.92771297 0.99119487 0.33149293]
[ 0.48005022 0.61086498 0.19062979]
[ 0.05214626 0.61618909 0.08295882]]
0.0521462614894 0.991194872459
☞ その13・・・要素の平均値(mean value)を出す
Z = np.random.random(3)
m = Z.mean()
print(Z)
print(m)
=>
[ 0.43252845 0.86545314 0.8868291 ]
0.728270233139
☞ その16・・・対角の1つ下の行列を作る、1~4、diagonal
Z = np.diag(1+np.arange(4),k=-1)
print(Z)
=>
[[0 0 0 0 0]
[1 0 0 0 0]
[0 2 0 0 0]
[0 0 3 0 0]
[0 0 0 4 0]]
☞ その17・・・チェックボードパターンの行列
Z = np.zeros*4
print(Z)
=>
[[0 1 0 1]
[1 0 1 0]
[0 1 0 1]
[1 0 1 0]]
☞ その20・・・Normalize(最大が1&最小が0になる)
Z = np.random.random*5
Zmax, Zmin = Z.max(), Z.min()
Z = (Z - Zmin)/(Zmax - Zmin)
print(Z)
=>
[[ 0.91425657 0.07881159 1. ]
[ 0.63918169 0.58862944 0.43357481]
[ 0.4049732 0.1090024 0. ]]
☞ その21・・・Create a custom dtype that describes a color as four unisgned bytes
☞ その22・・・Multiply a 5x3 matrix by a 3x2 matrix (real matrix product)
☞ その23・・・1~10のうち3~8をnegateする
Z = np.arange(11)
Z[(3 < Z) & (Z <= 8)] *= -1
print(Z)
=>[ 0 1 2 3 -4 -5 -6 -7 -8 9 10]
☞ その24・・・Consider an integer vector Z, which of these expressions are legal
☞ その27・・・How to round away from zero a float array ?
Z = np.random.uniform(-10,+10,10)
print (np.trunc(Z + np.copysign(0.5, Z)))
=>
[ -8. 4. 6. -3. 1. 4. 10. 2. -7. -8.]
☞ その28・・・整数部の抽出、やり方イロイロ
# 1~5のランダムな数を5つ持つ行列
Z = np.random.uniform(1,5,5)
print (Z)
# 整数の抽出
print (Z - Z%1)
print (np.floor(Z))
print (np.ceil(Z)-1)
print (Z.astype(int))
print (np.trunc(Z))
=>
[ 3.5029238 4.47885352 1.91640941 1.43928684 4.46256647]
[ 3. 4. 1. 1. 4.]
[ 3. 4. 1. 1. 4.]
[ 3. 4. 1. 1. 4.]
[3 4 1 1 4]
[ 3. 4. 1. 1. 4.]
☞ その29・・・5x5 matrix with row values ranging from 0 to 4
Z = np.zeros*6
Z += np.arange(5)
print(Z)
=>
[[ 0. 1. 2. 3. 4.]
[ 0. 1. 2. 3. 4.]
[ 0. 1. 2. 3. 4.]
[ 0. 1. 2. 3. 4.]
[ 0. 1. 2. 3. 4.]]
☞ その30・・・Consider a generator function that generates 10 integers and use it to build an array
◆行列&ベクトルに関する計算
☞ スカラー演算
W = np.array([[1, 2, 3], [4, 5, 6]])
x = np.array([7, 8, 9])
print(W * 2) #要素を2倍
print(-x) #要素にマイナス
=>
[[ 2 4 6]
[ 8 10 12]]
[-7 -8 -9]
☞ 行列を計算する際の方向 ”axis”

W = np.array([[1, 2, 3], [4, 5, 6]])
print(W.sum())
print(W.sum(axis=0))
print(W.sum(axis=1))
=>
21
[5 7 9]
[ 6 15]
◆行列の積 ”matmul”
(1)行列とベクトル
A = np.array([[2,3,4], [3,4,5]]) #行列
y = np.array([1,2,3]) #ベクトル
print(A)
print(y)
print(np.matmul(A, y))
=>
[[2 3 4]
[3 4 5]]
[1 2 3]
[20 26] #積の答え
(2)行列と行列
A = np.array([[2,3,4], [3,4,5]]) #行列
B = np.array([[2,3], [3,4],[4,5]]) #行列
print(A)
print(B)
print(np.matmul(A, B))
=>
[[2 3 4]
[3 4 5]]
[[2 3]
[3 4]
[4 5]]
[[29 38] #積の答え
[38 50]]
print(np.matmul(W, W.T))
print(np.matmul(W.T, W))
◆”dot”積
・行やベクトルしか関係しない計算であればmatmalとdotは差ナシ
A = np.array([[2,3,4], [3,4,5]])
B = np.array([[2,3], [3,4],[4,5]])
print(np.dot(A, B))
=>
[[29 38] #積の答え
[38 50]]
*1:2,3
*2:3,3,3
*3:3,3
*4:4,4),dtype=int)
Z[1::2,::2] = 1
Z[::2,1::2] = 1
print(Z)
=>
[[0 1 0 1]
[1 0 1 0]
[0 1 0 1]
[1 0 1 0]]
☞ その18・・・Consider a (6,7,8) shape array, what is the index (x,y,z) of the 100th element?
print(np.unravel_index(100,(6,7,8)))
=>
(1, 5, 4)
☞ その19・・・tileファンクションを使ってチェックボード
Z = np.tile( np.array([[0,1],[1,0]]), (2,2
*5:3,3
*6:5,5
TensorFlow(その1)
◆MNISTデータのダウンロード(jupyter)
☞ INTERFACE(2017年3月号の67ページ~写経)
・次のコードでデータダウンロード
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)

・4つのファイルがダウンロードされる。
◆画像データの中身
INTERFACE(2017年3月号の67ページ~)
(1)画像データの中身確認
mnist.train.images[0]

(2)その他
・ラベルデータ
mnist.train.labels[0]
・データの数の確認
mnist.train.num_examples
◆ソフトマックス関数
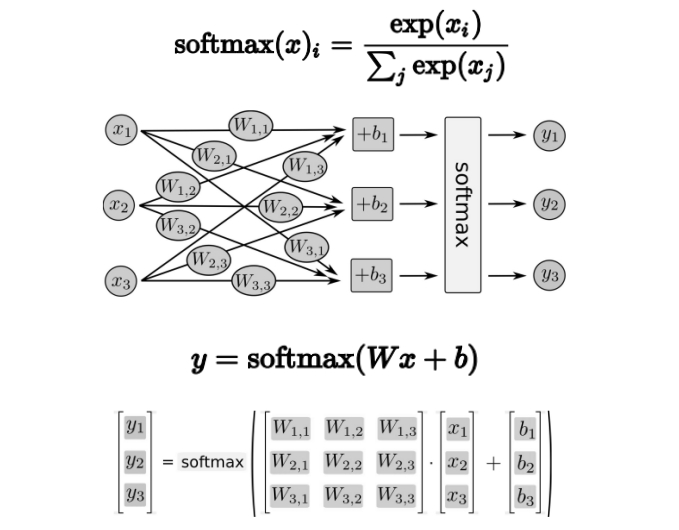
(2017.4.13.)
Matplotlibで画像を表示してみるetc(その1)
◆Python画像処理の写経
(1)画像を読み込んで表示する
import numpy as np
import matplotlib.pyplot as plt
img = plt.imread('***.jpeg')
plt.imshow(img)
plt.show()
(2)画像の保存
plt.imsave('***.jpeg', img)

◆Tips
・dtypeの指定 → 白黒では必要なし、カラーのとき使う)
・vmin/vmax → 白黒画像では必要。imshow()で勝手に正規化されないように。
・interpolation = 'none' → 勝手にかかるフィルターを外す
(3-2)RGB画像

◆Tips
・arrayの中身を変えることでRGBA画像(要素4つ)なども表示可能。
・”RGBA”の”A”は、透明度を表すアルファのA。
◆画像を拡大する
・"repeat"を使う
・縦5倍&横3倍にした例


《参考》
・Python画像処理の再発明家 ~行列による画像処理・基礎編&目次~ - Qiita
◆追加(2018-8-3)
(1)Google Colaboratory上でのsin波表示

code:
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(-5, 10, 0.1)
y = np.sin(x)
plt.plot(x, y)
※ jupyter notebookの場合、plt.show() つける
(2)色の指定
import matplotlib.pyplot as plt import numpy as np colorlist = ["r", "g", "b", "c", "m", "y", "k", "w"] x = np.arange(1, 9) height = np.repeat(1, 8) plt.bar(x, height, color=colorlist, tick_label=colorlist, align="center")

(2017-3-31)
(追記 2018-8-3)