WindowsにJupyterNotebookをインストールする（コマンドプロンプトより）

・コマンドプロンプトを立ち上げて下記コマンドを1つずつ入力

$ pip install -U pip
$ pip install jupyte

・コマンドプロンプトでjupyter notebookと打って起動。

↓

Keywords:
ジュピターノートブック、ウィンドウズ、pipインストール

（2018-7-27）

Google Colaboratoryを使ってみる

◆特徴
・Python、JupyterNotebookをブラウザ上で使える（PCの環境構築不要）。
・Tensorflow、Numpy、Matplotlib、Pandas、Keras、Chainer等が予め用意されている。
・GPU環境

その1. lena画像を表示する

・下記実行で画像をアップロードするためのアイコンが出てくる。

# 画像アップロード
from google.colab import files
uploaded = files.upload()

・アップされたようなので、これ↓で表示(^^

# 表示
from IPython.display import Image,display_jpeg
display_jpeg(Image('lena.jpg'))

その2. TensorFlowのtutrial（mnist）少しさわる

・手書き文字データのダウンロード→ ランダムに10個とって表示

import numpy as np
import matplotlib.pyplot as plt
from tensorflow.examples.tutorials.mnist import input_data

# mnistデータをダウンロード
mnist = input_data.read_data_sets("/tmp/data/", one_hot=True)

# 取出し 表示
images, labels = mnist.train.next_batch(10)

fig = plt.figure(figsize=(8,4))

for c, (image, label) in enumerate(zip(images, labels)):
    subplot = fig.add_subplot(2,5,c+1)
    subplot.set_xticks([])
    subplot.set_yticks([])
    subplot.set_title('%d' % np.argmax(label))
    subplot.imshow(image.reshape((28,28)), vmin=0,vmax=1, 
                   cmap=plt.cm.gray_r, interpolation="nearest")
plt.show()

その3. OpenCVも使えるみたい

・画像の顔認識モジュールを使う
　Qiita記事をみながら…
Colaboratory上でOpenCVを使って顔認識をしてみる

・OpenCV公式GitHubのカスケード分類器(haarcascade_frontalface_default.xml)をダウンロード → 上記同様のfiles.upload()でColaboratory上にファイルをアップロードする。その後下記実行。

import io
import numpy as np
import requests
import cv2
from matplotlib import pyplot as plt

# Web上の画像を読込み
res = requests.get('http://cinema.usc.edu/userfiles/A0127948311B99D1C02CF7783648D35EBD92E9B2images/Goonies2(1).jpg')

bin_data = io.BytesIO(res.content)
file_bytes = np.asarray(bytearray(bin_data.read()), dtype=np.uint8)

img = cv2.imdecode(file_bytes, cv2.IMREAD_COLOR)

# matplotで表示するためにBGR->RGBフォーマットに変換
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)

# アップロードした分類器ファイルを使用
cascade = cv2.CascadeClassifier('./haarcascade_frontalface_default.xml')

# 検出
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
face = cascade.detectMultiScale(gray, scaleFactor=1.1, minNeighbors=3, minSize=(30, 30))

# 検出した領域を矩形で囲む
for (x, y, w, h) in face:
  cv2.rectangle(img, (x, y), (x + w, y + h), (200,0,0), 3)

# xy軸ラベル非表示
plt.grid(False)
plt.tick_params(labelbottom=False, labelleft=False, labelright=False, labeltop=False)
plt.imshow(img)

その4. Chainerも使える？？

・Coraboratory上で次のようなインストールが必要とのこと

!apt-get install -y -qq libcusparse8.0 libnvrtc8.0 libnvtoolsext1
!ln -snf /usr/lib/x86_64-linux-gnu/libnvrtc-builtins.so.8.0 /usr/lib/x86_64-linux-gnu/libnvrtc-builtins.so
!pip install cupy-cuda80==4.0.0b4 
!pip install chainer==4.0.0b4

その5. データのプロットの近似直線の表示

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

# numpyを使ってデータ生成
x = np.linspace(0,1,30)
y = np.random.rand(30)

# フィッティング直線
a, b = np.polyfit(x, y, 1)
y2 = a * x + b

# 表示関連
fig=plt.figure()

ax=fig.add_subplot(111)
ax.scatter(x,y,alpha=0.5,color="Purple",linewidths="1")
ax.plot(x, y2,color='Blue')

ax.text(0.1,a*0.1+b, 'y='+ str(round(a,4)) +'x+'+str(round(b,4)))

plt.show()

・Colaboratory上のグラフ表示

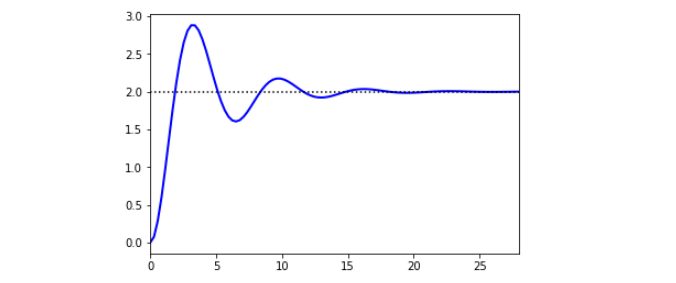
その6-1. Pythonを使って制御（一次遅れ系）のプロット描画

from sympy import *
from pylab import *

# 一次遅れ系 伝達関数 G(s)=K/(T*s+1), (T>0, K>0)
K,T = symbols('K T', positive=True)
s,t = symbols('s t')
G = Lambda((s, K, T), K/(T*s+1))

# ステップ応答信号 u(t)=1  ラプラス変換
U = Lambda(s, laplace_transform(1, t, s)[0]) # U(s)=1/s

# 一次遅れ系の単位ステップ応答 y(t) はY(s)=G(s)*U(s)=K/(s*(T*s+1)) の逆ラプラス変換
ilt = inverse_laplace_transform
y = Lambda((t, K, T), ilt(G(s,K,T)*U(s), s, t))

# K=1, T=5 の場合をプロット
trange = arange(0, 45, 0.1)
plot(trange, [y(t,1,5) for t in trange])
plt.axhline(1, color="gray", linestyle="--")

show()

・表示結果

その6-2. 二次遅れ系のプロット描画

・とりあえず写経

import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
from scipy.integrate import odeint

%matplotlib inline

# tau * dy2/dt2 + 2*zeta*tau*dy/dt + y = Kp*u

Kp = 2.0    # gain
tau = 1.0   # time constant
zeta = 0.25 # damping factor
theta = 0.0 # no time delay
du = 1.0    # change in u

# Transfer Function

num = [Kp]
den = [tau**2,2*zeta*tau,1]
sys1 = signal.TransferFunction(num,den)
t1,y1 = signal.step(sys1)

plt.figure(1)
plt.plot(t1,y1*du,'b-',linewidth=2,label='Transfer Fcn')

y_ss = Kp * du

plt.plot([0,max(t1)],[y_ss,y_ss],'k:')
plt.xlim([0,max(t1)])

plt.show()

・表示結果

・参考：
https://apmonitor.com/pdc/index.php/Main/ModelSimulation

その7. Fashionmnist+KerasのNN

・ファッションmnistを使った簡単なニューラルネットワークの学習

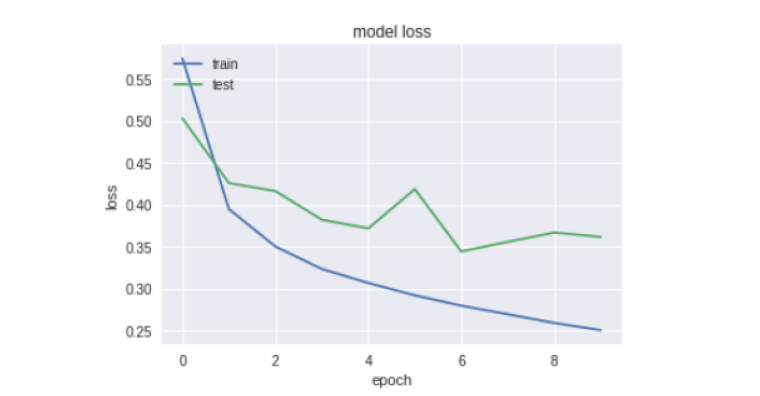
# 参考： http://uchidama.hatenablog.com/entry/2018/01/18/064500

# import libraries 
import keras
import matplotlib.pyplot as plt
import numpy as np
import random
from matplotlib import cm
%matplotlib inline

# import modules# impor 
from __future__ import print_function
from keras.datasets import fashion_mnist

# the data, shuffled and split between train and test sets
(x_train, y_train), (x_test, y_test) = fashion_mnist.load_data()

print('x_train shape:', x_train.shape)
print(x_train.shape[0], 'train samples')
print(x_test.shape[0], 'test samples')

print('x_train shape:',x_train.shape)
print('y_train shape:',y_train.shape)
print('x_test shape:',x_test.shape)
print('y_test shape:',y_test.shape)

print(type(x_test))
print(type(y_test[0]))

# show sample data、見てみる
fig = plt.figure(figsize=(9,9))

for i in range(25):
    ax = fig.add_subplot(5, 5, i+1, xticks=[], yticks=[])
    ax.imshow(x_train[i], cmap='gist_gray')

# 前処理
# reshape 28*28 pixel data into 784 dim data
# convert into float type and normalize pixel data from 0.0 to 1.0
x_train = x_train.reshape(60000, 784).astype('float32') /255
x_test = x_test.reshape(10000, 784).astype('float32') /255

# encode label data into "one-hot" 
y_train = keras.utils.np_utils.to_categorical(y_train.astype('int32'),10)
y_test = keras.utils.np_utils.to_categorical(y_test.astype('int32'),10)

# モデルの層構造
# 2層のニューラルネットワーク、ドロップアウト無し
# 一般的なmnistの分類器ででf_mnistも分類できる

# Sequential Model# Sequen 
from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation
from keras.optimizers import RMSprop

# neural network structure
model = Sequential()
# 1st layer
model.add(Dense(100, activation='relu', input_shape=(784,)))
# 2st layer
model.add(Dense(100, activation='relu'))
# 3st layer
model.add(Dense(10, activation='softmax'))

# 学習
# Set definitions for traning
model.compile(loss='categorical_crossentropy',
              optimizer=RMSprop(),
              metrics=['accuracy'])

# Excute training for 10(epochs) times
history = model.fit(x_train, y_train, batch_size=128, epochs=10, verbose=1, validation_data=(x_test, y_test))

# 結果表示
# plot the resulut
plt.plot(history.history['acc'])
plt.plot(history.history['val_acc'])
plt.title('model accuracy')
plt.ylabel('accuracy')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper left')
plt.show()


# plot the loss
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper left')
plt.show()

[google colaboratory、コラボレイトリー、Jupyter Notebook、Tensorflow、チュートリアル、画像表示、ファイルアップロード、ダウンロード、mnist]

2018-5-16

Python 基本構文のメモ

◆ IF文
（1）変数ｘ、ｙの合計が20本より多いかどうかで条件分けして、表示内容を変える。

x = 15
y = random.choice([4, 5])  
print('x=' + str(x))
print('y=' + str(y))

if x + y < 20:
    print('20本注文する')
else:
    print('注文しない')

◆ 比較演算子
・「==」・・・等しい
・「!=」・・・等しくない

（2）偶数か奇数かを判定するプログラム
・2で割って余りがゼロかどうかで条件分けをする。

import random  
x = random.choice([4, 5])  

if x % 2 == 0:
    print('xは偶数')
else:
    print('xは奇数')

機械学習 Machine Learningの基本的な考え方（数学etc）

◆目的：
・機械学習における数学的なモデルとか誤差関数、学習etcのキホンを確認。

◆機械学習の3ステップ
・数式モデル→誤差関数→パラメータ調整

◆線形分離の例
・例えば感染or非感染を直線で分離する場合には、下記の式を使う。

　 y=ax+bのような形式ではない（x1とx2を対称に扱うためとのこと）

● f（x1,x2）の関数の特徴
　- この値がゼロなら直線上。
　- 値が大きくなるほど直線から離れていく。

● このように用意した関数 f（x1,x2）と感染確率の関係は？

・「×」側に離れると確率が1.0に近づき、「○」側に離れると0に近づくような関数σ（x）を使う。

◆キーワード：
［機械学習、モデル、線形分離、loss function、パラメータ、感染確率P］

◆参考：
・中井悦司、「TensorFlowで学ぶディープラーニング」、マイナビ、22ページ

（2017.9.4.）

Python XORゲートをSVMで学習させる（「Pythonによるスクレイピング＆機械学習」150ページ）

◆目的：
・XORゲートをSVMで学習させる。

◆XORゲート
・排他的論理和の論理ゲート。

◆コード全体

#socym本の写経、p.150 2017-9-1
#サポートベクターマシンsvmのインポート
from sklearn import svm

#データの用意
xor_data = [
    [0, 0, 0],
    [0, 1, 1],
    [1, 0, 1],
    [1, 1, 0],
]

data = []
label =[]

#インプットと正解とを分ける 
#1行目から順に要素を抜きリストに追加していく(？)
for row in xor_data:
    x = row[0]
    y = row[1]
    z = row[2]
    data.append([x,y])
    label.append(z)

#どんな感じになっているか一旦表示
print("data の中身=>", data) 
print("labelの中身=>",label)

#svmアルゴリスム利用
#svmのオブジェクトを得て、fitメソッドでデータを学習
#fitメソッド・・・（データ配列，ラベル配列）
clf =  svm.SVC()
clf.fit(data,  label)

#データの予測
#predictメソッド・・・予測したいデータ配列を与えると、データの数だけ予測を返す
pred = clf.predict(data)
print("予測結果=", pred)

結果：
data の中身=> [[0, 0], [0, 1], [1, 0], [1, 1]]
labelの中身=> [0, 1, 1, 0]
予測結果= [0 1 1 0]

◆キーワード：
［scikit-learn、サイキットラーン、svm、fitメソッド、predictメソッド、機械学習、XOR演算］

◆参考：
・「Pythonによるスクレイピング＆機械学習」、150頁～、ソシム本

（2017.9.1.）

Python 関数について

◆目的：
関数がどのようなものか確認する。

◆関数について
・書式

def 関数名（引数）:
　　処理

● returnって?
・関数の計算結果を返す。

例：関数 y=x^2 があるとして、x=1,2のときの出力の和 f(1)+f(2)を求める。

def f(x):
    return x ** 2

print (f(1)+f(2))

⇒ 出力：5

(画像参考)

Tensorflow 計算のきほん

◆目的：
・tensorflowでの計算の基本的な考え方を確認する

◆例：「ａ＋ｂ」の足し算をする
・例えば、

　　　10＋20＝30

　 を計算させる。

・変数vを定義して"10+20"の値を代入して表示
・tensorflowでの処理の流れはこんな感じ

◆コード（その1）

import tensorflow as tf

a = tf.constant(10)
b = tf.constant(20)
v = tf.Variable(0)

sum = a + b

assign = tf.assign(v, sum)#vに10+20の結果を代入している

sess = tf.Session()
sess.run(tf.global_variables_initializer())
sess.run(assign)

結果：

◆コード（変数vを使わない単純な足し算）

import tensorflow as tf

a = tf.constant(10)
b = tf.constant(20)

sum = a + b

sess = tf.Session()
sess.run(sum)

結果：

◆例：空の配列に数値データを与えて２倍にするプログラム
・プレースホルダにリストの値を与える。

import tensorflow as tf

a = tf.placeholder(tf.int32,[3])#要素が3つの整数の配列
b = tf.constant(2);
enzan_x2 = a*b

sess = tf.Session()
r1 = sess.run(enzan_x2, feed_dict={ a:[10,15,30]})
print(r1)

結果：
[20 30 60]

※Memo:
・要素の数を「3」に固定したが、固定しない場合は”None”

tf.placeholder(tf.int32,[None])

◆参考：
・「Pythonによるスクレイピング＆機械学習」、205頁-、ソシム

（2017.7.26.）

追記（2017.8.19.）

Python import文について

◆import sysって？
・sysモジュール（様々な変数や関数が含まれている）をインポートしている。sysモジュール以下すべての変数＆関数を“sys.を先頭に付ける形で利用できるようする。
・ちなみにimport文は、import {.pyを除いたファイル名}構文

>>>import sys

◆たとえばどんな感じ？

☞ print(sys.path)
・sys.pathはpythonパス（PYTHONPATH）をリストにして返す。絶対パスの文字列リスト。
・「path 変数は、モジュール検索パス、すなわちPythonがモジュールのインポート時にモジュールの検索対象とするディレクトリーのリストです。1個目の空文字列'' は、カレント・ディレクトリーを表します。」＠IBMウェブサイト

>>>print(sys.path)

☞ print(sys.version)
・pythonやanacondaのバージョンを表示。

>>>print(sys.version)

◆とりあえず手を動かして"import"に慣れるコード書いてみる

●目的：
・mainプログラムにmoduleプログラムを読み込んで動かす
・天気予報をランダムに表示 （O'REILLY入門Python3の139ページ）

●予め用意するmoduleプログラム
・文字列のリストからランダムに1つを選択。
・tenkiyosoku.pyという名前で所定のディクトリに保存。
・なお、 randomモジュール＆choice関数はputhon標準

def get_yosoku():
    from random import choice
    possibilities = ['晴れ','雨','曇り','雪']
    return choice(possibilities)

●mainプログラム
・moduleプログラムにアクセスし、その中のget_yosoku()関数を実行する。
・一行目を過ぎ一旦インポートされてしまえば、［moduleプログラム］名のプリフィックスを付けてmoduleプログラムの全ての部分にアクセスできる。

import tenkiyosoku

description = tenkiyosoku.get_yosoku()

print('実行のたびランダムに天気表示するよ:', description)

結果：

◆ Memo:
・sys.path…中身はリスト。os.path…モジュール。
・参考にしたサイト IBMウェブサイト
https://www.ibm.com/developerworks/jp/linux/library/l-pyint/index.html

（2017.7.24.）

Tensorflow ORゲートのモデルの機械学習（詳解デープラーニング3章）

◆目的：
・ORゲートの分離境界モデルを学習させる
・巣籠本（2017）の93ページ～

◆ORゲート
・いずれか一方の入力が1であれば、出力が1となる回路。

・大まかな流れ

◆実装：
（1）まずいつもの

import numpy as np
import tensorflow as tf

（2）パラメータの定義
・こんな感じ

x = tf. placeholder(tf.float32, shape=[None, 2])
w = tf.Variable(tf.zeroｓ([2,1]))
b = tf.Variable(tf.zeros([1]))
y = tf.nn.sigmoid(tf.matmul(x,w) + b)

tf. set_random_seed(0)#乱数シード

（3）学習のときに使うパラメータt

t = tf.placeholder(tf.float32, shape=[None, 1])

（4）誤差関数は交差エントロピー

cross_entropy  = - tf.reduce_sum(t * tf.log(y) + (1 -t) * tf.log(1-y))

（5）学習の式

train_step = tf.train.GradientDescentOptimizer(0.1).minimize(cross_entropy)

（6）予測

correct_prediction = tf.equal(tf.to_float(tf.greater(y,0.5)),t)

（7）X,Y

X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
Y = np.array([[0], [1], [1], [1]])

（8）初期化

init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)

（9）学習、200回まわす
・Tensorflowでは、Sessionで計算を実施

for epoch in range(200):
    sess.run(train_step, feed_dict={
        x: X,
        t: Y
    })

（10）学習結果の確認
・evalは発火/非発火の分類確認
⇔ tf.Variableの変数の値はevalでなくsess.run()で取得

classified = correct_prediction.eval(session=sess, feed_dict={
    x: X,
    t: Y
})
prob = y.eval(session=sess, feed_dict={
    x: X
})

print('classified:')
print(classified)
print()
print('output probability:')
print(prob)

（11）結果はこんな感じ↓

・学習されたパラメータを確認
　縦ベクトルwの中の値2つが下記のように学習されたことが確認可能。

print('w:', sess.run(w))

→ w: [[ 3.61188436]
　　[ 3.61188436]]

◆Memo:
・パラメータbの値…print('b:', sess.run(b))で確認できる。

◆キーワード：
ORゲート、分離境界、ランダム、乱数データ、学習率、学習されたパラメータの確認

** 以上 **

（2017.7.17.）

Tensorflowインストール（windows）

◆ 目的：
・Tensorflowのインストール

◆ 環境
・Windows10
・Python、Anaconda環境は構築済み

（1） 以下のコマンドを実行

pip install tensorflow

（2017.7.17.）

Keras インストール〜幾つか

◆ インストール（Mac）

pip install keras

Matplotlibに慣れる（データのプロット、グラフ表示etc）

◆目的：
データのプロットやグラフを表示する

◆練習いろいろ
1. グラフの表示etc
（1）10個の乱数データを生成してグラフにプロットする。

import numpy as np
import matplotlib.pyplot as plt

・乱数の生成、分散図、ラベル

#.randは0～1の範囲で乱数生成

x = np.random.rand(10)
y = np.random.rand(10)

plt.scatter(x, y)
plt.xlabel("X"), plt.ylabel("Y")

plt.show()

（2）折れ線
・分散図 scatterではなく、次のようにすると折れ線になる。

plt.plot(x, y)
plt.show()

2. 数式→表示
（1）1次関数

def formura(x):  
    return 2*x + 50

x = np.arange(-10.0, 10.0, 1.0) #マイナス10からプラス10まで1刻み
y = formura(x)

plt.plot(x,y)
plt.show()

（2）アークタンジェント

x = np.arange(-10, 10, 0.1)
y = np.arctan(x)

plt.plot(x, y)

(3) 二次関数 y=x^2

x = np.arange(-9.5, 10, 0.5)
y = x ** 2
 
plt.figure()
plt.xlim(-10.0, 10.0)
plt.ylim(-10, 100.0)

plt.grid(True)

plt.plot(x, y)
plt.show()

（3）y=logx 自然対数
・Cf. 交差エントロピー誤差

x = np.arange(0,0.99,0.01)
y = -np.log(x)

plt.plot(x,y)
plt.show()

**追加予定**

◆Memo:
（1）jupyter notebookでノート上にグラフ表示
・インライン表示の一文をいれておく

%matplotlib inline

（2）画像の保存etc

plt.savefig('./graph.png', dpi=100)

◆キーワード：
python、matplotlib、pandas、データプロット、データ表示、分散図、グラフ

Chainer インストール〜サンプルプログラムの実行

【MacOS、Sierra、Chainer、wget1.16、インストール】

◆ 目的（その1）：
Chainerをインストールしてサンプルプログラムを動かすところまで。

1. Chainerをインストール
・chainer 2.0.0

$ pip install chainer

2. Chainer公式サンプルプログラムを実行
（1）サンプルプログラム実行のコマンドにwgetというのが出てくるけど、mac ターミナルでは”wget”コマンドが使えないようなので対処

まず、wgetが既に入っているかを確認。

$ which wget

→ 対処
・Homebrewのインストール（公式ホームページ）

$ /usr/bin/ruby -e "$(curl -fsSL https://
　　　raw.githubusercontent.com/Homebrew/install/master/install)"

以下がインストールされる
/usr/local/share/doc/homebrew
/usr/local/share/man/man1/brew.1
/usr/local/share/zsh/site-functions/_brew
/usr/local/etc/bash_completion.d/brew
/usr/local/Homebrew

・brew install でwgetを入れる

$ brew install wget

⇒ 解決

（2）Chainer公式のサンプルプログラム実行
・MNISTの識別のプログラムらしい..

wget https://github.com/pfnet/chainer/archive/v2.0.0.tar.gz
tar xzf v2.0.0.tar.gz
python chainer-2.0.0/examples/mnist/train_mnist.py

MacBookAirではエポックを回すのにかなり時間がかかるけど、一応、少しずつ精度が上がっていっている模様。

**以上**

※ 参考にしたサイト
・Homebrew — macOS 用パッケージマネージャー
・Macにwgetコマンドをインストールしてみる - kengo92iの日記

◆ 目的（その2）：
・WindowsにChainerをインストールする

→ 仮想環境VirturalBoxにUbuntuを入れて実行する とのこと

　　　（追記予定...）

Tensorflow ロジスティック回帰による二項分類器（マイナビ本参考）

◆ 目的：
ウィルスの感染を分類する、したい。

◆ キーワード：
ロジスティック回帰、二項分類器、境界線、直線、確率0.5、シグモイド関数、データのランダム生成、確率の最大化、最尤推定法、統計学、誤差関数、log、pandas、DateFrame、行列T、ブロードキャスト、グラフの描画、濃淡、スパム、感染非感染、学習

・まずは、インポート・準備

# ロジスティック回帰の二項分類器、65頁参考

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt

# 乱数を使ってデータ生成、pandasのデータフレームとして格納

from numpy.random import multivariate_normal, permutation
import pandas as pd
from pandas import DataFrame, Series

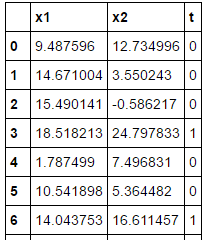
・感染データ/非感染データを作る

# データを用意
# 感染していないデータ（t=0）の生成

np.random.seed(20170602)

n0, mu0, variance0 = 20, [10, 11], 20
data0 = multivariate_normal(mu0, np.eye(2)*variance0 ,n0)
df0 = DataFrame(data0, columns=['x1','x2'])
df0['t'] = 0

# 感染しているデータ（t=1）の生成
n1, mu1, variance1 = 15, [18, 20], 22
data1 = multivariate_normal(mu1, np.eye(2)*variance1 ,n1)
df1 = DataFrame(data1, columns=['x1','x2'])
df1['t'] = 1

df = pd.concat([df0, df1], ignore_index=True)

# データセット
# 上で生成したデータを表示して内容を確認、３５コのサンプルデータ

train_set = df.reindex(permutation(df.index)).reset_index(drop=True)
train_set

・変数を定義

# Tensorflowで計算できるようにデータを変形
# numpyのarrayオブジェクトとして変数に格納
# X・・・（ｘ１ｎ、ｘ２ｎ）の行列　、　ｔ・・・正解ラベル

train_x = train_set[['x1','x2']].as_matrix()
train_t = train_set['t'].as_matrix().reshape([len(train_set),1])

# Step１_予測のための数式定義
#　確率Pを行列形式で計算
# f = x*w + w0
# 入力データは３５行２列 but Noneでサイズ規定
# ｗは、ｗ　=　（ｗ１，ｗ２）T 転置 ・・・横のw１、ｗ２を縦に並べている　２行１列
# w０は、ブロードキャスト・・・１次元リストでも足せる
# ｔｆ．sigmoidはそれぞれの入力に対するシグモイド関数の一次元リスト

x = tf.placeholder(tf.float32, [None, 2])
w = tf.Variable(tf.zeros([2,1]))
w0 = tf.Variable(tf.zeros([1]))

f = tf.matmul(x,w) + w0

p = tf.sigmoid(f)

・誤差関数を定義

# Step2_誤差関数定義
# 数式自体は-logPを掛け合わていくような複雑なやつ,Σで表現＠p７０
# tf. reduce_sumは和集約

t= tf.placeholder(tf.float32, [None, 1])
loss = -tf.reduce_sum(t*tf.log(p) + (1-t)*tf.log(1-p))

# アダムオプティマイザーで上で定義したloss関数を最小化していく

train_step = tf.train.AdamOptimizer().minimize(loss)

・予測

#　正解ｏｒ不正解の分別 Pn＞＝0.5であればｔ＝１
#  tf.sign  符号を取り出す関数
# tf.equal  引数が等しいかを判定する関数 Bool値を返す
# ブロードキャストルールによって、Bool値の縦ベクトルが生成される

correct_prediction = tf.equal(tf.sign(p-0.5), tf.sign(t-0.5))

# tf．cast　　Bool値を１，０の値に変換
# tf.reduce_mean  ベクトルの各成分の平均値、正解なら１、不正解なら０

accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))

#　パラメータの最適化
sess = tf.Session()
sess.run(tf.global_variables_initializer())

・勾配降下法

# 勾配降下法 ２００００回繰り返し

i = 0
for _ in range(20000):
    i += 1
    sess.run(train_step, feed_dict={x:train_x, t:train_t})
    
    if i % 2000 == 0:
        loss_val, acc_val = sess.run([loss, accuracy], feed_dict={x:train_x, t:train_t})
        print('Step: %d, Loss %f, Accuracy: %f' % (i, loss_val, acc_val))

（out）
Step: 2000, Loss 16.098034, Accuracy: 0.857143
Step: 4000, Loss 12.176691, Accuracy: 0.885714
Step: 6000, Loss 9.802266, Accuracy: 0.914286
Step: 8000, Loss 8.280571, Accuracy: 0.914286
Step: 10000, Loss 7.283283, Accuracy: 0.914286
Step: 12000, Loss 6.632703, Accuracy: 0.914286
Step: 14000, Loss 6.220951, Accuracy: 0.914286
Step: 16000, Loss 5.976564, Accuracy: 0.914286
Step: 18000, Loss 5.848728, Accuracy: 0.914286
Step: 20000, Loss 5.797661, Accuracy: 0.942857

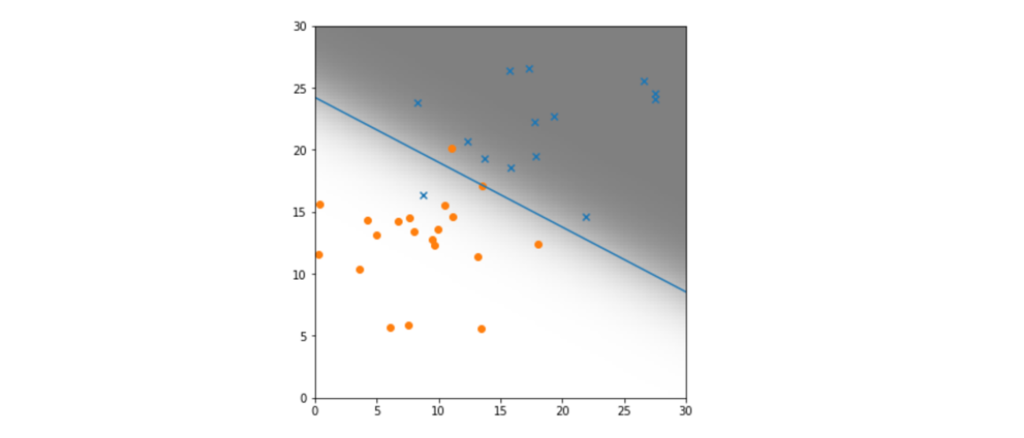
# Variableの値を取得
# w0・・・１要素のみのリスト
# ｗ　・・・２行１列の行列
# ［０］［０］は一行目を取り出し、［１］［０］は２行目を取り出し

w0_val, w_val = sess.run([w0, w])
w0_val, w1_val, w2_val = w0_val[0], w_val[0][0], w_val[1][0]

print (w0_val, w1_val, w2_val)
-14.9617 0.322867 0.617867

# 結果をグラフに表示
# 境界線は、P（ｘ１，ｘ２）=０．５ の確率
#　シグモイド関数はロジスティック関数とも。ロジスティック回帰。

#トレーニングセットのデータからt=０、１のデータを個別に取出し

train_set0 = train_set[train_set['t']==0]
train_set1 = train_set[train_set['t']==1]

#　散布図の記号etc

fig = plt.figure(figsize=(6,6))
subplot = fig.add_subplot(1,1,1)
subplot.set_ylim([0,30])
subplot.set_xlim([0,30])
subplot.scatter(train_set1.x1, train_set1.x2, marker='x')
subplot.scatter(train_set0.x1, train_set0.x2, marker='o')

・グラフの細かい描画設定

# 境界線の直線の描画

linex = np.linspace(0,30,10)
liney = - (w1_val*linex/w2_val + w0_val/w2_val)

subplot.plot(linex, liney)

# 確率の変化を濃淡で示す
# （ｘ１，ｘ２）平面を１００ｘ１００のセルに分割
# それぞれのセルの確率P(ｘ１、ｘ２)の値を２次元リスト filedに格納　濃淡表示

field = [[(1 / (1 + np.exp(-(w0_val + w1_val* x1 + w2_val*x2))))
         for x1 in np.linspace(0,30,100)]
        for x2 in np.linspace(0,30,100)]

subplot.imshow(field, origin= 'lower', extent = (0,30,0,30), cmap=plt.cm.gray_r, alpha=0.5)

plt.show()

Tensorflow 身長・体重・BMIの学習（ソシム本、218ページ）

# 2017-5-21 ソシム スクレイピング本
# 218ページ〜 BMI計算、CSVファイル
# 予め用意したCSVファイルを使って、BMI分類を学習
# 交差エントロピ、ソフトマックス、勾配法

import pandas as pd
import numpy as np
import tensorflow as tf

# 身長,体重,ラベルのCSVデータを読み出す 
# pandas でCSVファイル読み出し
csv = pd.read_csv("bmi.csv")

# データを正規化 、０〜１に
csv["height"] = csv["height"] / 200
csv["weight"] = csv["weight"] / 100

# ラベルを三次元のクラスで表す --- (※3)
# 痩せ、普通、肥満を３つの三次元クラスデータで表す
# thin=(1,0,0) / normal=(0,1,0) / fat=(0,0,1)

bclass = {"thin": [1,0,0], "normal": [0,1,0], "fat": [0,0,1]}
csv["label_pat"] = csv["label"].apply(lambda x : np.array(bclass[x]))

# 正解率を求めるためにテストデータを準備 
# ２万件のうち末尾５０００件をテストデータにする

test_csv = csv[15000:20000]
test_pat = test_csv[["weight","height"]]
test_ans = list(test_csv["label_pat"])

# データフローグラフを構築する
# データを入れるプレースホルダを宣言

x  = tf.placeholder(tf.float32, [None, 2]) # 身長,体重のデータを入れる
y_ = tf.placeholder(tf.float32, [None, 3]) # 答えのラベルを入れる

# 変数を宣言 --- (※6)
W = tf.Variable(tf.zeros([2, 3])); # 重み
b = tf.Variable(tf.zeros([3])); # バイアス

# ソフトマックス回帰を定義 
# y=softmax(Wb+b)
y = tf.nn.softmax(tf.matmul(x, W) + b)

# モデルを訓練する
cross_entropy = -tf.reduce_sum(y_ * tf.log(y))

# 降下法でWやbを学習する、tfに用意されているもの
optimizer = tf.train.GradientDescentOptimizer(0.01)
train = optimizer.minimize(cross_entropy)

# 正解率を求める
# 誤差関数：交差エントロピー
# SummaryWriter

predict = tf.equal(tf.argmax(y, 1), tf.argmax(y_,1))
accuracy = tf.reduce_mean(tf.cast(predict, tf.float32))

# セッションを開始
sess = tf.Session()
sess.run(tf.global_variables_initializer()) #変数を初期化

# テストデータを用いて学習させる、１００件ずつ３５００回学習
# 最初３０%くらいの正解率が、９５％くらいまで向上

print("- トレーニング中 -")

for step in range(3500):
    i = (step * 100) % 14000
    rows = csv[1 + i : 1 + i + 100]
    x_pat = rows[["weight","height"]]
    y_ans = list(rows["label_pat"])
    fd = {x: x_pat, y_: y_ans}
    sess.run(train, feed_dict=fd)
    if step % 500 == 0:
        cre = sess.run(cross_entropy, feed_dict=fd)
        acc = sess.run(accuracy, feed_dict={x: test_pat, y_: test_ans})
    
        print("step=", step, "cre=", cre, "acc=", acc)

# =>
- トレーニング中 -
step= 0 cre= 109.101 acc= 0.3084
step= 500 cre= 52.4673 acc= 0.8688
step= 1000 cre= 46.4283 acc= 0.9226
step= 1500 cre= 38.8364 acc= 0.9472
step= 2000 cre= 35.4385 acc= 0.9588
step= 2500 cre= 31.0386 acc= 0.9494
step= 3000 cre= 31.2941 acc= 0.9532

# 最終的な正解率を求める

acc = sess.run(accuracy, feed_dict={x: test_pat, y_: test_ans})

print("正解率=", acc)
# =>
正解率= 0.966